Multi-Scale Derivative
We use an integrated multi-scale derivative, multi-source, and multi-level approach to estimate horizontal boundaries, depth, and SI at all the scales and depths resolvable within the field.
We use an integrated multi-scale derivative, multi-source, and multi-level approach to estimate horizontal boundaries, depth, and SI at all the scales and depths resolvable within the field.
Our approach is based on a weighted sum of the enhanced multi-scale derivative – a high resolution boundary estimator based on the horizontal derivative of a weighted sum of vertical derivatives.
The multi-level multi-scale derivative provides estimates of source depth, density contrast and structural index from spectra, analytic signal, tilt-derivative and Euler deconvolution.
The bulk of the information in both gravity and magnetic fields are contained in the derivatives of the field, fusing the horizontal and vertical derivatives, help to highlight discontinuities.
Gravity and magnetic multi-scale derivative interpretation of potential fields convey source information depending on the scale at which the field derivative is analyzed. Multi-scale derivative analysis is useful when the main field contributions are caused by sources of different depths and extents.
Our multi-scale derivative approach (both horizontal and vertical) is built from a stable vertical integral transformation of the field, since traditional filtering processes introduce distortions in the field and an arbitrary ‘regional’ and ‘local’ definition. Far superior are multi-scale derivative methods, based on the properties of field vertical derivatives, which perform a consistent and non-arbitrary separation.
The main difficulty in gravity and magnetic interpretation is due to reciprocal interference of source edges. We estimate source boundaries by the multi-scale derivative analysis of the vertical field, producing a set of boundary maps at different scales. Integrating multi-scale derivatives (horizontal and vertical ) results in retrieval of information of the field sources (horizontal boundaries, depth, and structural index).
Adding higher order vertical multi-scale and multi-level derivatives significantly contributes more detail to the shallow sources such as fault edges and improves gravity and magnetics interpretations.
The combination of these vertical derivatives with the horizontal derivative – the EHD method – suppresses the noise characteristics of the field. For example, the low order terms may include also the first vertical integral of the field, which places field detail in a regional-scale context for easier interpretation. After Fedi (2002), we use these features to design specific tools for projects that produce meaningful maps of structural lineaments relative to different scales without performing any subjective processes.
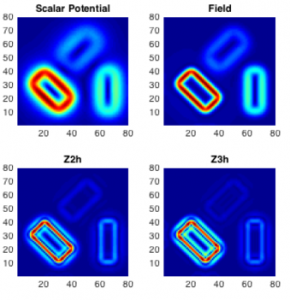
By adding higher-order enhanced vertical derivative terms using the EHD method, detail of the shallower sources is obtained. A set of weights controls the relative importance of the terms of the summation. The use of the highest order vertical derivatives is in practice limited by the data sampling step.
EHD significantly reduces the risk of working with pseudo-anomalies introduced from a noise boost and so strengthens the gravity and magnetics interpretation.
The availability of data sets at different levels from ground, ship-borne, airborne, and satellite gravity and magnetics surveys allows the fusion of results from gravity and magnetic interpretation of potential fields analyses from different heights, and so overcomes the need for arbitrary and problemmatic wavelength-filtering.
The effects of the varying terrain are minimized and the major and deeper features are enhanced relatively to the effects of shallower features.
Models can be tested against these multi-level data sets, decreasing the uncertainty of the solutions.
Blakely R.J. and Simpson R.W. 1986. Approximating edges of source bodies from magnetic or gravity anomalies. Geophysics 51,1494-1498.
Carrozzo, M. T., Luzio, D., Margiotta, C., and Quarta, T., 1986, Gravity anomaly map of Italy. Progetto Finalizzato Geodinamica – Sottoprogetto: Modello Strutturale Tridimensionale: Rome, Italy
Cooper, G. R. J., and D. R. Cowan, 2006. Enhancing potential field data using filters based on the local phase: Computers & Geosciences 32, 1585-1591
Fairhead J.D. and Williams S.E., 2006, Evaluating normalized magnetic derivatives for structural mapping. SEG Expanded Abstracts 25, 845
Fedi M., 2002. Multi-scale Derivative Analysis: a new tool to enhance gravity source boundaries at various scales, Geophysical Research Letters, 29, 16-1 to 16-4
Fedi, M., 2007, DEXP: A fast method to determine the depth and the structural index of potential fields sources. Geophysics 72, I1-I11.